How To Set Up A Ratio Problem

Solving Proportions: Similar Figures

Some other category of proportion trouble is that of "similar figures".

"Like" is a geometric term, referring to geometric shapes that are the same, except that one is larger than the other. Think of what happens when you use the "enlarge" or "reduce" setting on a copier, or when y'all get an 8-by-x enlargement of a picture y'all really similar, and you'll have the right idea; or, if you've used a graphics program, think "aspect ratio".

Content Continues Below

In the context of ratios and proportions, the point of similarity is that the corresponding sides of like figures are proportional; that is, that the lengths are proportional.

For example, look at the similar triangles ABC and abc beneath:

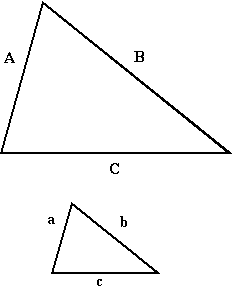
The "respective sides" are the pairs of sides that "match", except for the enlargement or reduction attribute of their relative sizes. Then A corresponds to a , B corresponds to b , and C corresponds to c .

Since these triangles are similar, and so the pairs of respective sides are proportional. That is, A :a =B :b =C :c . This proportionality of corresponding sides can be used to find the length of a side of a figure, given a similar figure for which the measurements are known.

• In the displayed triangles, the lengths of the sides are given past A = 48 mm, B = 81 mm, C = 68 mm, and a = 21 mm. Observe the lengths of sides b and c , rounded to the nearest whole number.

I'll set up my proportions, using ratios in the course (big triangle length) / (minor triangle length), so I'll solve the proportions. Since I have merely the length of side a for the petty triangle, my reference ratio volition exist A :a .

Offset, I'll notice the length of b . Here's my fix-up:

Filling in my known values, I get:

(I'll need to remember to give the rounded-to-whole-number for (namely, "35") in my hand-in reply.)

Now that I've found one length, I will, by the aforementioned method, find the length of the remaining side, c .

For my respond, I could but slap downwardly the two numbers I've plant, but those numbers won't make much sense without their units. Also, in re-checking the original exercise, I'grand remindedthat I'thousand supposed to round my values to the nearest whole number, then "29.75", with or without units, would exist incorrect. The right answer is:

b = 35 mm, c = 30 mm

---

While I could have used the length I'd institute for b for finding the length of c in the above practise, I instead returned to the value of a . Why? Because it was a known-skilful "exact" value. hile the decimal value was in this case an exact value (that is, the value for b was not rounded), it's mostly better to make a habit of returning to known-good values, whenever yous tin. That way, when a decimal value has been rounded, y'all're ignoring the rounded derived value and returning to the verbal original value. This practice will help yous avert circular-off error.

---

• A picture measuring 3.5" (that is, 3.v inches) high by 5" wide is to be enlarged so that the width is at present ix". How tall will the movie be?

The photograph lab, when enlarging the original picture, will exist maintaining the aspect ratio of the original; that is, the rectangles representing the outer edges of the original and enlarged pictures volition be like figures. Using this fact, I can set up up a proportion and solve, using " h " to represent the summit value that I'm seeking:

The height of the picture volition exist:

6.iii inches

---

In the first do higher up, the ratios were between respective sides, and the proportionality was formed from those pairs of sides. The ratios in the proportions independent fractions formed from the original large value divided by the new small value. In the second exercise above, the ratios were between the two different dimensions, and the proportionality was formed from the sets of dimensions. The ratios in the proportion contains fractions formed from the old peak and old width, and from the new peak and the new width.

For many exercises, you lot will be able to ready up your ratios and proportions in more than 1 way. This is perfectly okay. Just make sure that you label things well, clearly ascertain your variables, and set things upwardly in a sensible and consequent manner. Doing so should help yous dependably achieve the correct solutions. If you're ever non sure of your solution, recall to plug information technology back into the original exercise, and verify that it works.

---

There is another topic, kind of an off-shoot of similar-figures questions, which you lot may encounter. It is the fact that, if ii figures (or iii-dimensional shapes) are similar, and then non only are their lengths proportional, simply so also are their squares (being their areas) and their cubes (being their volumes).

• Two rectangular prisms are similar, with one pair of respective lengths being 15 cm and 27 cm, respectively. (a) If the volume of the smaller prism is 2000 cm³, what is the book of the larger prism? (b) If the area of ane confront of the larger prism is 243 cm², what is the area of the corresponding side of the smaller prism?

A "rectangular prism" is just fancy geometrical talk for "a brick", so I know that I'yard working with iii-dimensional shapes. I am given that the shapes are similar, and I'yard provided with two comparative lengths. This gives me my basic ratio:

This is the linear ratio for the two prisms, and it'due south what I'll use for finding my answers for volume and surface area.

(a) To find the volume of the larger prism, I demand to cube the linear ratio they gave me (that is, I need to cube the reduced fraction that I'd created when I'd put the two lengths into a ratio, above). Putting the values for the smaller prism in the tops of the ratios, this gives me:

This is the ratio I'll use for setting up my volume proportion:

Checking my units, I go an answer of:

(a) 11,664 cmⁱⁱⁱ

(b) To observe the surface area of the i side of the smaller prism, I demand to square the linear ratio they gave me (that is, I need to foursquare the reduced fraction created past putting the 2 lengths into a ratio). Putting the values for the smaller prism in the tops of the ratios, this gives me:

This is the ratio I'll employ for setting upwards my surface area proportion.

Checking my units, I get an answer of:

(b) 75 cmⁱⁱ

How To Set Up A Ratio Problem,

Source: https://www.purplemath.com/modules/ratio6.htm

Posted by: charleypaptur.blogspot.com

Share this post